|
| 1 | +# Counting Sort |
| 2 | + |
| 3 | +In computer science, **counting sort** is an algorithm for sorting |
| 4 | +a collection of objects according to keys that are small integers; |
| 5 | +that is, it is an integer sorting algorithm. It operates by |
| 6 | +counting the number of objects that have each distinct key value, |
| 7 | +and using arithmetic on those counts to determine the positions |
| 8 | +of each key value in the output sequence. Its running time is |
| 9 | +linear in the number of items and the difference between the |
| 10 | +maximum and minimum key values, so it is only suitable for direct |
| 11 | +use in situations where the variation in keys is not significantly |
| 12 | +greater than the number of items. However, it is often used as a |
| 13 | +subroutine in another sorting algorithm, radix sort, that can |
| 14 | +handle larger keys more efficiently. |
| 15 | + |
| 16 | +Because counting sort uses key values as indexes into an array, |
| 17 | +it is not a comparison sort, and the `Ω(n log n)` lower bound for |
| 18 | +comparison sorting does not apply to it. Bucket sort may be used |
| 19 | +for many of the same tasks as counting sort, with a similar time |
| 20 | +analysis; however, compared to counting sort, bucket sort requires |
| 21 | +linked lists, dynamic arrays or a large amount of preallocated |
| 22 | +memory to hold the sets of items within each bucket, whereas |
| 23 | +counting sort instead stores a single number (the count of items) |
| 24 | +per bucket. |
| 25 | + |
| 26 | +Counting sorting works best when the range of numbers for each array |
| 27 | +element is very small. |
| 28 | + |
| 29 | +## Algorithm |
| 30 | + |
| 31 | +**Step I** |
| 32 | + |
| 33 | +In first step we calculate the count of all the elements of the |
| 34 | +input array `A`. Then Store the result in the count array `C`. |
| 35 | +The way we count is depected below. |
| 36 | + |
| 37 | +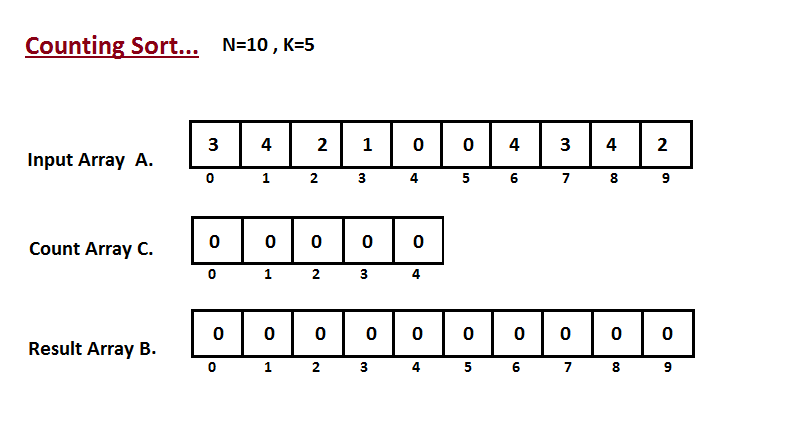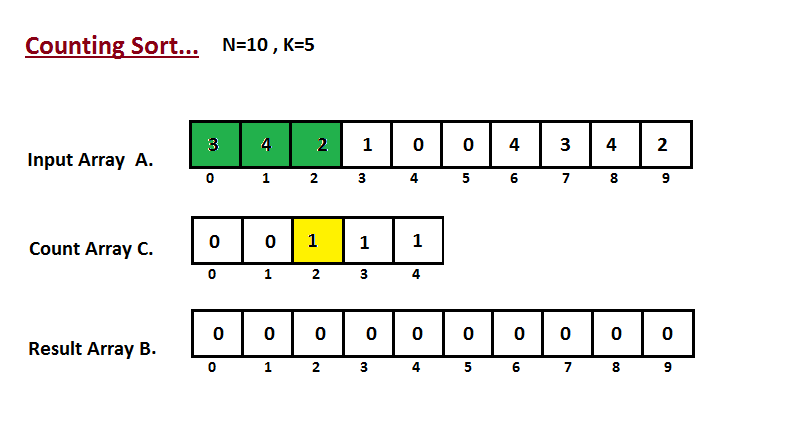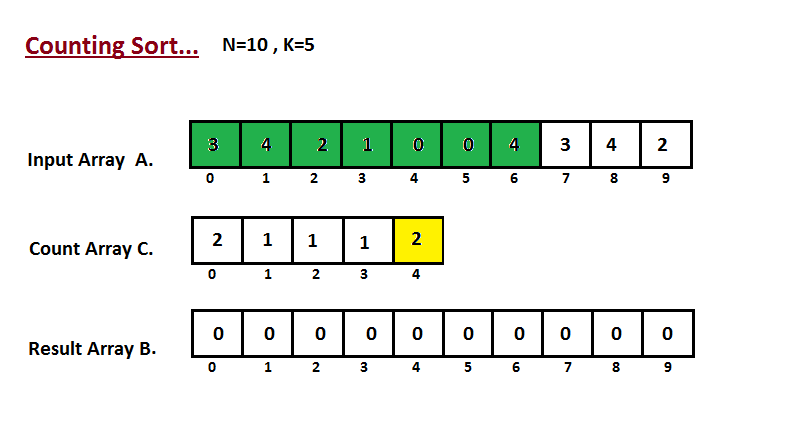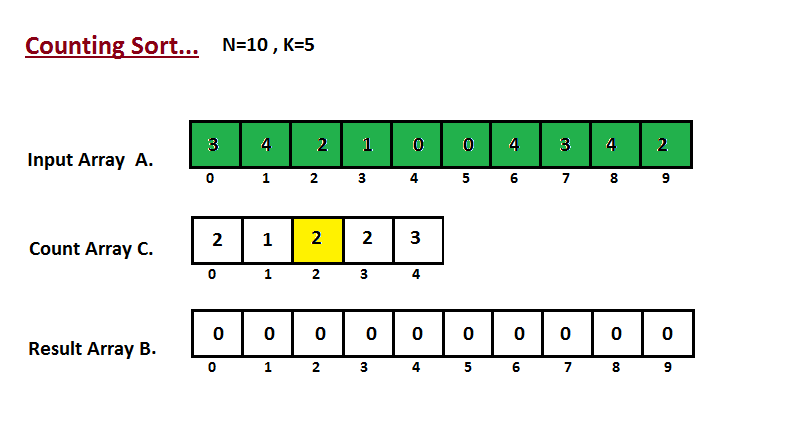 |
| 38 | + |
| 39 | +**Step II** |
| 40 | + |
| 41 | +In second step we calculate how many elements exist in the input |
| 42 | +array `A` which are less than or equals for the given index. |
| 43 | +`Ci` = numbers of elements less than or equals to `i` in input array. |
| 44 | + |
| 45 | +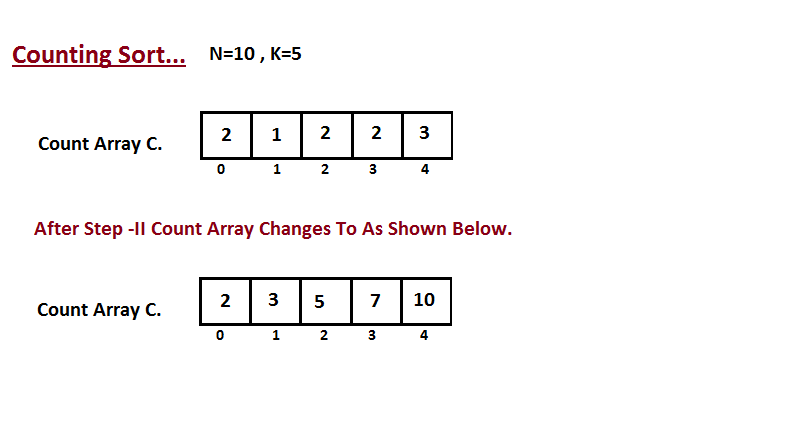 |
| 46 | + |
| 47 | +**Step III** |
| 48 | + |
| 49 | +In this step we place the input array `A` element at sorted |
| 50 | +position by taking help of constructed count array `C` ,i.e what |
| 51 | +we constructed in step two. We used the result array `B` to store |
| 52 | +the sorted elements. Here we handled the index of `B` start from |
| 53 | +zero. |
| 54 | + |
| 55 | +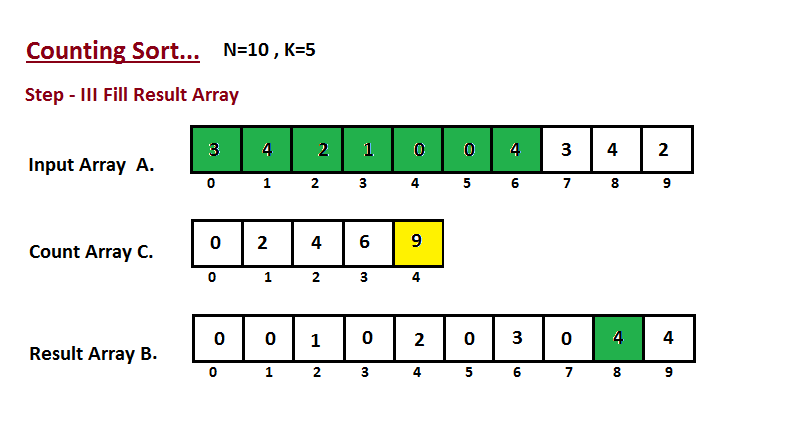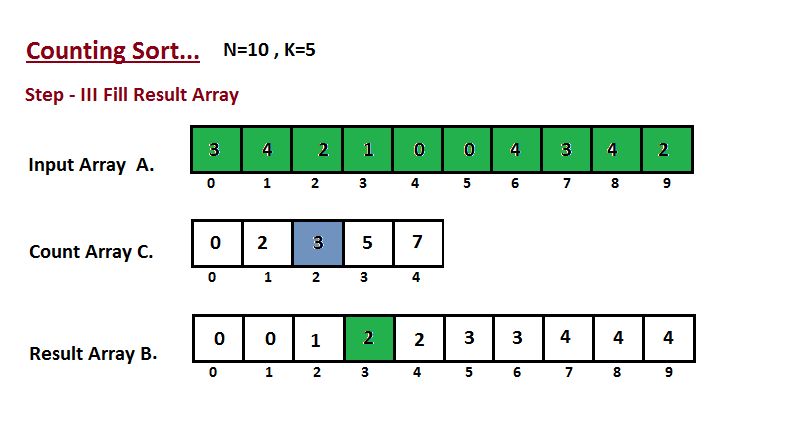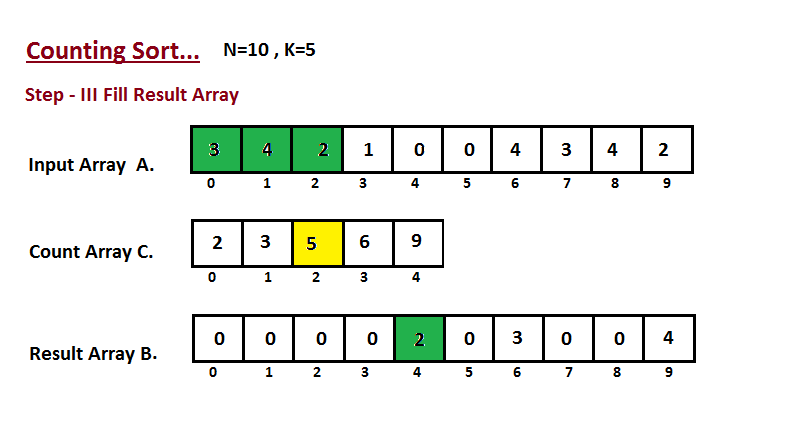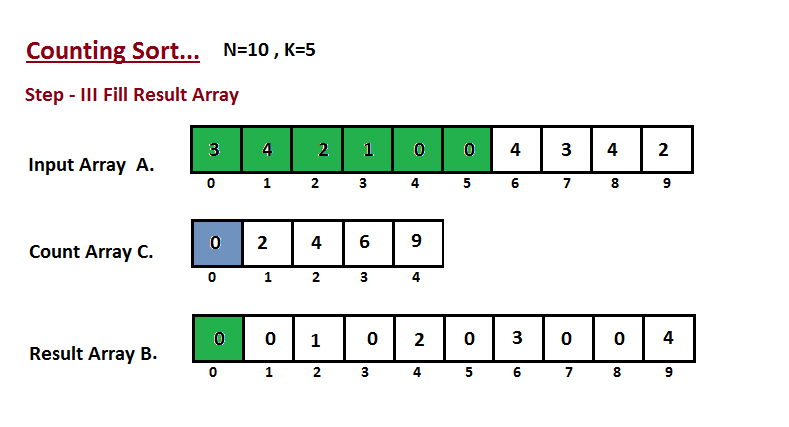 |
| 56 | + |
| 57 | +## References |
| 58 | + |
| 59 | +- [Wikipedia](https://en.wikipedia.org/wiki/Counting_sort) |
| 60 | +- [YouTube](https://www.youtube.com/watch?v=OKd534EWcdk&index=61&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) |
| 61 | +- [EfficientAlgorithms](https://efficientalgorithms.blogspot.com/2016/09/lenear-sorting-counting-sort.html) |
0 commit comments